Place Value Digits Worksheets
When we are given an integer the value of the digits within the integer can greatly differ. For instance, in the number 4758 the value of digit 4 (4000) is 80 times greater than the digit 5 (50). This is due to the base ten number system that we follow. If you are given a continuous set of integers each digit is ten times as you move from left to right. As you move right to the left in that same integer the worth of each digit is ten times greater. Below you will find a series of worksheets and lessons that help students appraise the worth of an integer found within a larger number based on place value. We will mostly work up to the thousands place and down to the thousandths place. You will find that we jump around more in advanced practice sheets.
Aligned Standard: 4.NBT.2
- What's the Number Step-by-Step Lesson- We describe the integers at set place values. You tell us the number that we are describing.
- Place Patterns Step-by-Step Lesson- Now we have you break apart the places of number groups.
- Guided Lesson - Both skills from the lessons are mixed in here.
- Guided Lesson Explanation - You will see the use of a top-down strategy used here. Students find this to be very effective.
- Independent Practice Worksheet 1 - I threw a ridiculously high amounts on problem number 6. Kids do take a long look at that one.
- Independent Practice Worksheet 2 - We stick with small amounts to work with here to help you refine your skills.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
We did get a reference to this homework in an academic journal, in a good way.
- Homework 1 - A number has the following integers at the following place values: 8 in the tenths, 9 in the hundreds, 7 in the ones, and 3 in the tens. What is the number?
- Homework 2 - Find the highest and lowest place values of the number. Place the integers at their proper location based on this information.
Practice Worksheets
Practice makes perfect!
- Practice 1 - Circle the number that has an 8 at the thousands place.
- Practice 2 - Start by identifying the highest and lowest digit that is available.
- Practice 3 - Now let's remind ourselves of the place values between those digits that are present.
Math Skill Quizzes
Once students have mastered this skill, they should move on to higher place values.
- Quiz 1 - What is the number?
- Quiz 2 - Circle the number that has an 8 at the hundredths place.
- Quiz 3 - Circle the number that has a 6 at the tenths place.
How to Spot the Place Value of a Digit?
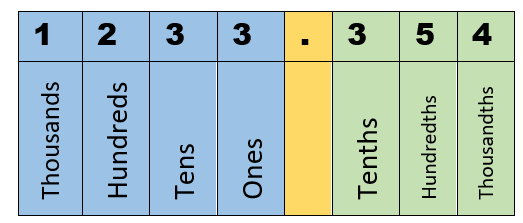
One of the most important concepts in mathematics is, of course, place values. Every digit found within an integer holds a unique worth. Without these values, a digit has no meaning. It helps in comparing two numbers and finding which number is larger or smaller. The leading zeros are the only digits that have no value. What is extremely unique to our base ten system is that every successive digit is either ten times greater or less than the previous location. If you move to the right digits become ten times less than the previous position. The opposite is true of the digits as you move to the left, they are ten times greater than their previous positions.
Spotting place values within numbers are easy. The only rule in with this concept is to start assigning the place values from the first digit on the right side. For example, if you must assign place values to the digits of the number 564382. You will start assigning the place value from 2, which sits at the unit place. That integer (2) would indicate the ones place and it would increase from there.
When dealing with decimal numbers, you have to assign place values for the integer that lies exactly on the left side of the decimal. Consider a number 2318.231. To assign place values, you can create a table and start assigning the values. Start by identifying the location of the decimal point. All the integers to the left of that point are whole numbers, the first integer indicating the ones place. All of the integers to the right of the decimal point are fraction pieces (less than one), starting at the tenths place.
Naming the positions of each integer are fixed in place follow a systematic pattern. The basic flow of the names of these places are listed below. If you have a good handle of those that are listed below you should be in good shape to tackle most of the problems that you will come across.