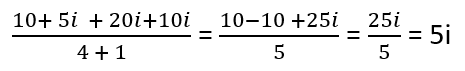Conjugates and Dividing Complex Numbers Worksheets

This is a purposefully pairing of topics because you can not technically divide complex numbers. That is because you can only divide anything by real numbers and the imaginary number portion of complex numbers invalidates your ability to do that. How we achieve this is by first writing the quotient as a fraction and then if we determine the conjugate of the denominator, we can multiple both the numerator and denominator by the conjugate. This will result in the denominator being a real number by getting rid of the imaginary portion. This series of worksheets and lesson will first get us comfortable with determining the conjugate and then we will apply it to dividing complex numbers.

Aligned Standard: HSN-CN.A.3

• Complex Quotients Step-by-step Lesson- When division isn't all about remainders or carrying the one.
• Guided Lesson - Find two conjugates and one quotient. A bit detailed though.
• Guided Lesson Explanation - I try to break it down into simple concepts for you.
• Practice Worksheet - Six conjugates and four quotients for you to work with.
• Matching Worksheet - Match the conjugates, quotients and the numbers that started it all off for you.

• Answer Keys - These are for all the unlocked materials above.

Homework Sheets

We start with finding the quotients of complex numbers. We finish off with determining conjugates.

• Homework 1 - To find conjugates remember,: The conjugate of a + bi = a – bi
• Homework 2 - Use the form we just learned in action.
• Homework 3 - Multiply the top and bottom by the conjugate.

Practice Worksheets

Time to work on some crazy division that you never thought was possible.

• Practice 1 - Determine the conjugate of the denominator.
• Practice 2 - Find the conjugates of: 5 + 25i
• Practice 3 - Do not forget to simplify at the end.

Math Skill Quizzes

Some of the questions work off of one another. See if that works for you.

• Quiz 1 - This is all in on conjugates.
• Quiz 2 - There are operations included with these.
• Quiz 3 - A nice solid way to end it all off.

What is a Math Conjugate?

The word conjugate is used in usually two contexts, in mathematics. One, when working with binomials which are half rational and half irrational numbers. Other times, a conjugate is used in the context when dealing with binomials which are again partially rational and partially imaginary. But normally, a math conjugate is when we change the middle sign found between two terms. It is a way of changing the very nature of operation that is involved between the two terms. For example: The conjugate of 3x + 1 is 3x - 1.

This is extremely helpful when you are working with fraction that exhibit a root in the denominator. It can often help you rationalize such situations and help you achieve a balanced number to work on forward with. It also helps you equalize expressions that might exhibit opposite operations, but the same terms.

How Divide Complex Numbers

The division of complex numbers, well it is pretty complicated, to say the less. It is not much different than performing the same operation with real numbers. It all begins with you writing the problem in fraction form first. Then you multiply both the numerator and denominator by the conjugate of the denominator and solve it from there. That is because technically you cannot divide complex numbers, but you rearrange them as conjugates and go crazy from there. Let's explore this by Dividing 5 + 10i by 2 – i.

Step 1) Write it as a fraction.

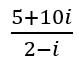
Step 2) Find the conjugate of the denominator and multiply the numerator and denominator by that conjugate.

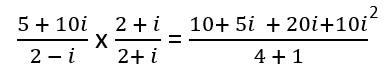
Step 3) Simplify the fraction and write the solution in form a + bi.