Vector Magnitude and Direction Worksheets

Vectors are often used to model the movement and to analyze the forces that are at work to create this motion. The basic elements of a vector are the direction of the force that is signified by the direction that the arrow points and the magnitude (intensity) that is signified by the length of the line segment from the head of the arrow to the tail. If we are able to find two points that begin and end the vector using a coordinate system, we could easily determine these measures using the distance formula. We would need some information in order to determine the direction of the motion though. These worksheets and lessons show you how to find sums between vectors in the way of both magnitude and direction.

Aligned Standard: HSN-VM.B.4b

• Visualizing Vector Sums Step-by-step Lesson- I give you a word problem that will prompt you to draw the vectors first.
• Guided Lesson - This is where you might start to lose some students. Make sure that they understand every step along the way.
• Guided Lesson Explanation - I tried to make this very clear. I might have added an extra step or two.
• Practice Worksheet - This one can be very time consuming. It took one of my students just under an hour to complete it.
• Matching Worksheet - Match the vector word problem to its outcome.

• Answer Keys - These are for all the unlocked materials above.

Homework Sheets

For this skill we compound two calculations to get a better understanding of the vector.

• Homework 1 - Find the supplementary angle to find an angle of the triangle.
• Homework 2 - Use the Law of cosines to find the direction.
• Homework 3 - Find the measurement of the angle between the vector of the 15 pounds and the vector of the 20 pounds force to the nearest whole degree.

Practice Worksheets

We now translate this skill to real world word problems.

• Practice 1 - Two forces with magnitudes of 21 pounds and 23 pounds are applied to the same fixed object. The magnitude of the resultant force is 10 pounds. Find the measurement of the angle between the resultant vector and the vector of the 21 pounds force to the nearest whole degree.
• Practice 2 - A vector u has a magnitude of 10 and a direction of 0°. A vector v has a magnitude of 20 and a direction of 30°. Find the direction and magnitude of u +v to the nearest whole values.
• Practice 3 - Round to the nearest whole degree as needed.

Math Skill Quizzes

Make sure to review the use of angles in these. The angle 0° seems to give kids trouble and trips them up.

• Quiz 1 - Use the Law of cosines, substitute the values and simplify.
• Quiz 2 - Find out what you can on the u vector.
• Quiz 3 - These will help you understand the overall process of what is being talked about here.

How to Find Vector Sums of Magnitude and Direction

Mathematical operations on vectors are usually common when you are learning advanced mathematics or working in a physics classroom. One of the basic mathematical operations used often with vectors is the concept of finding sums of multiple vectors which requires the addition operation. This allows you to understand the net force that is present in a real-world motion scenario. You can add two vectors to determine the resultant (or result) of the two vectors. However, it is important to understand that direction plays an important part in finding out the result of adding two vectors.

Let us consider an example, and if you are moving a box of books horizontally, then the applied force is in the direction parallel to the x-axis. However, if you apply the force from upwards, the direction is downwards, and the box stays at the same place.

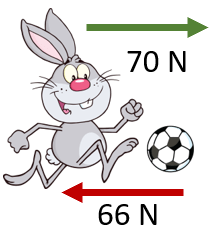
Let us take another example. Thomas and Clark play soccer for two different teams during physical education class in school. During an exhibition match, they came head-to-head and kicked the ball simultaneously in the opposite direction. Thomas kicked the ball with a force of 66N, while Clark kicked it with a force of 70N. Find out the net force of the ball.

Now, there are two forces acting on the ball. Thomas standing at one end applies a force of 66N on it, while the strong Clark kicked it back with 70N. That means Thomas' kick canceled out the force of Clark's kick. The force of Thomas and Clark's kicks are denoted by T and C respectively.

Resultant = C + T: Due to the opposite direction of the forces, the resultant will consist of vector subtraction. Resultant=C+(-T) | Resultant=70 - 66 | Resultant = 4N. The direction of the force is Clark's kick due to its increased value.